Pico is a tiny but expressive programming language that was designed to teach advanced computer science concepts to students in other sciences than computer science. This page contains a brief overview of Pico intended for programming language experts. It is certainly not meant as a Pico tutorial.
In Pico the basic syntactical entities are - not unexpectedly - numbers (i.e. integers), fractions (i.e. reals), texts, Scheme-style symbols, variable definitions, variable references, function definitions and function applications. Texts are specified as double quote-delimited character strings while numbers and fractions follow the generally accepted rules. Variables are alphanumerical strings starting with a letter, or, operator character sequences (see later). Every isolated instance of the name of a variable constitutes a reference to it; defining a variable is done by associating it with an initial value:
Pi: 3.14159 fruit01: 'orange firstName: "Theo"
Function applications are formulated in elementary calculus style:
min(f(x),0)
i.e. a name followed by a parenthesis-delimited, comma-separated argument list. Functions are defined by associating an implementation with a function application prototype:
min(x,y): if(smaller(x,y),x,y)
Function names are extended to cover operators. Any function whose name is a combination of one or more symbols from the set {$, %, +, -, |, ~, &, *, \,/, !, ?, ^, #, <, =, >} is considered to be an operator. Unary or binary operators may be invoked in prefix or infix notation, again to reflect elementary calculus. For instance
x<<n: x*2^n 255<<4 !n : if(n=0,1,n* !(n-1)) !5
illustrates the definition and application of a shift operator and a factorial operator. Precedence among operators is determined by each operator's initial character and is hardwired into the syntax. There are four operator sets:
In general X > M > A > R. Operators are nothing more than syntactic sugar and do not have any impact on Pico's semantics. For the evaluator, operators are just plain functions. The infix appearance and the precedence is purely a syntactic matter.
The above examples define new names (i.e. variables or functions). It is also possible to declare them. Declaration is exactly the same as definition except for the fact that definition introduces assignable names whereas declaration introduces immutable (i.e. constant) names. Hence, only defined names can be re-assigned a new value later on. Declaration syntax is exactly the same as definition syntax except for the fact that a double colon is used:
Pi::3.1415
immutableFun(x)::x
In the spirit of Scheme, we have opted for a functional, dynamically typed, statically scoped language. There are, however, two major differences at the level of the basic semantics.
In the first place, we impose universal naming of functions:
comb(p,q): fac(p)/(fac(q)*fac(p-q))
defines the expression to the right of the colon as the implementation of a function called comb taking p and q for arguments. Compared to Scheme this absence of anonymous functions slightly reduces the expressiveness of Pico but eliminates most of the confusing recursion-related issues in Scheme such as the let, let* and letrec variants of block structures.
In the second place we extend the Scheme-like argument binding rule to include formal functional parameters. For instance:
and(p,q()):: if(p,q(),false)
defines a lazy Boolean function and.
Evaluating the expression:
and(a>0,a<10)
will result in the value of a>0 being bound to p and q to be bound to the definition of a parameterless function q(): a<10. Laziness results from q being called only when needed.
Formal functional parameters allow us to bypass the need for Scheme's special forms and to have totally uniform function call semantics. It was for instance very straightforward to introduce a lambda-calculus styled Boolean system:
true(then(), else()):: then() false(then(), else()):: else() and(left, right()):: left(right(), false) or(left, right()):: left(true, right()) not(pred):: pred(false, true) if(cond, then(), else()):: cond(then(), else())
The (informal) semantics of Pico expressions with respect to an environment env are extremely simple:
EVAL(x,env) = x if x is a number, a fraction, a text, a symbol or void.
EVAL(var:ini,env) = DEFINE(var,EVAL(ini,env),env)
EVAL(var::ini,env) = DECLARE(var,EVAL(ini,env),env)
EVAL(var,env) = LOOKUP(var,env)
EVAL(fun(arg...):bod ,env) = DEFINE(fun,FUNCTION(arg...,bod,env),env)
EVAL(fun(arg...)::bod ,env) = DECLARE(fun,FUNCTION(arg...,bod,env),env)
EVAL(fun(arg...),env) = APPLY(LOOKUP(fun,env),arg...,env)
In the above the DEFINE and LOOKUP functions act upon the environment in the usual way; FUNCTION and APPLY are identical to their Scheme equivalent, apart from the argument binding behaviour:
BIND(frm,act,env,callenv)
The names frm and act denote respectively a formal and actual parameter; env represents the (extended) static environment and callenv represents the dynamic environment. This part of the (informal) semantics constitutes the major difference with Scheme; it is also the basis for the uniform function call semantics of Pico.
With Pico's target audience in mind, we have taken a pragmatic approach to data structures. We opted for simple arrays called tables, which again according to Webster's is a systematic arrangement of data. A Pico table is represented using an additional syntactical notation which again as closely as possible reflects convention. A table is an indexable structure of fixed size; for instance:
primeNumbers[N]: true
defines a table called primeNumbers of size N and with all members initialised to the value of true. Indexing is e.g. performed as follows:
primeNumbers[2*k+1]
with the index expression 2*k+1 dynamically checked to range from 1 through N.
Members of a table are arbitrary combinations of valid Pico values, i.e. numbers, symbols, functions, tables and void. This closely reflects the data structure called vector from Scheme. In order to complete this picture, we also introduce destructive operations:
primeNumbers[4]:= false
rebinds the fourth member of primeNumbers to the value of false. In order to maintain consistency, we have therefore also included destructive operations for variables and functions:
Pi:=3.14159265358979
comb(p,q):= (fac(p)/fac(p-q))/(fac(q)
Notice that these assignements will only work when Pi and comb were previously defined instead of declared. Declared names are immutable!
Just like functions and variables, tables can also be declared. However, this does not mean that the table becomes immutable. The table reference itself cannot be changed. But the elements of the table can!
Conceptually, tables are one-dimensional, but a table can also contain tables. Since programs dealing with such "multi dimensional" tables easily get verbose (because one needs a temporary variable to read a higher dimension), multi dimensional table syntax a la t[1,2,3] was introcuced. However, an expression like t[1,4,2] is actually syntactic sugar for t[1][4][2] which is, as we will see, a more fundamental expression kind in Pico.
A Pico interpreter is understood to operate upon an abstract grammar representation of a Pico program. In the spirit of Scheme (where evaluation consist of List Processing), this abstract grammar is expressed as Pico tables; this makes it possible for us to define Pico in a metacircular way. A side-effect of this approach is that function argument lists are also represented as tables, which enables us to introduce functions with variable sized argument lists at no extra cost. Representing this operator by the symbol @, we can for instance define:
begin@list: list[size(list)]
i.e. a function begin taking at least one argument and returning the value of the last argument. Since (non-functional formal) parameter binding is eager in Pico and since argument passing always proceeds from left to right, the begin function defines the equivalent of a Scheme expression sequence and consequently:
loop(value, boolean): boolean(loop(body(), cond()), value)
defines an iterator. Using functional formal parameters we easily get:
while(cond(),body()): loop(void, cond())
Another useful application of @ is the following function:
table@list: list
which enables us to define tables in an alternative way:
primeNumbers:table(true,true,true,false,true,false,true,false,false)
In analogy to Scheme, @ can also be used to dynamically assemble function calls:
cell(start):
begin(put(command,value):start:=value,
get(command): start,
dispatch@message:
begin(op:if(message[1]='put,put,get),
op@message))
This example also shows that Scheme's higher- order function features have been retained in Pico: It defines a function cell whose body defines three local functions put, get and dispatch. The result of cell is the result of the last subexpression of the begin, i.e. the result of the definition of dispatch. The body of dispatch shows how the arguments of dispatch (variable number!) are simply passed onto put or get by the apply operator @. The right hand side of that apply operator should be an expression that results in a table of Pico values whose length is equal to the number of arguments expected by the function resulting from evaluating the left hand side.
The elementary examples of recursion are obviously very straightforward:
fac(n):: if(n>1, n*fac(n-1), 1)
but in Pico, it is also very easy to express more sophisticated algorithms in, such as for instance the quicksort:
QuickSort(V,Low,High)::
begin(Left:Low,
Right:High,
Pivot:V[(Left+Right)//2],
until(Left>Right,
begin(while(V[Left]<Pivot,Left:=Left+1),
while(V[Right]>Pivot,Right:=Right-1),
if(not(Left>Right),
begin(Save:V[Left],
V[Left]:=V[Right],
V[Right]:=Save,
Left:=Left+1,
Right:=Right-1),
false))),
if(Low<Right,QuickSort(V,Low,Right),false),
if(High>Left,QuickSort(V,Left,High),false))
Usign table to create tables, and especially, using begin to group expressions soon leads to extremely verbose programs. Therefore Pico allows for square brackets to group values (separated by commas) to be collected in a table, and, allows for curly braces to group expressions (separated by semi colons) to be executed one after the other. A table is thus created by enumerating its constituents:
t: [1,"hello", 2.3, sin, 'grandMaConcept,"last element" ]
and the above quicksort example is reformulated as:
QuickSort(V,Low,High)::{
Left:Low;
Right:High;
Pivot:V[(Left+Right)//2];
until(Left>Right,{
while(V[Left]<Pivot,Left:=Left+1),
while(V[Right]>Pivot,Right:=Right-1),
if(not(Left>Right),
{ Save:V[Left],
V[Left]:=V[Right],
V[Right]:=Save,
Left:=Left+1,
Right:=Right-1},
false)));
if(Low<Right,QuickSort(V,Low,Right),false);
if(High>Left,QuickSort(V,Left,High),false)}
However, this is mere syntactic sugar. The Pico parser replaces square brackets by a call of the table function. Likewise, curly braces are replaced by a begin call.
A Pico expression is always evaluated with respect to an environment consisting of the variable bindings "currently" in the scope. In Pico nomenclature, this environmnet is called the dictionary. The dictionary can be conceived as a linked list associating names with values. Adding a new name to the dictionary always happens at the end of the linked list and looking up a name always starts at the ebd of the list and proceeds upward. Conceptually, the dictionary is a linked list of mutable and immutable names which arise from definitions and declarations. Like anything else in Pico, these dictionaries are first class and syntax and native functions exist for manipulating them. The "current" dictionary is grabbed by calling the capture() native function with no arguments. The result is a dictionary that exposes a number of names. By definition, only the names that were declared (i.e. the immutable names) can be accessed from a dictionary. Trying to refer to a defined name will generate an error. This scoping mechanism allows us to create modules or even simple objects in Pico. The following code excerpt shows how these dictionaries are used in conjunction with a qualified dot operator to access the declared names of a dictionary.
{ Stack()::{
stk:void;
psh(e)::
stk:=[e,stk];
pop() ::
if(is_void(stk),
error("pop from empty stack"),
{ e:stk[1];
stk:=stk[2];
e });
capture() };
s1::Stack();
s1.psh(2);
s1.pop()}
The example shows a "constructor" function Stack that defines a local variable stk and declares two functions. Then the "current" dictionary is grabbed by calling capture() and returned from the constructor function. The two dot qualification expressions show how the declared names can be used in the dictionary.
Pico was conceived using only a very small set of rules. However, these rules are followed throughout the design in a very consistent and rigid way and it is really important to have them in mind constantly when reading about Pico. Here they are:
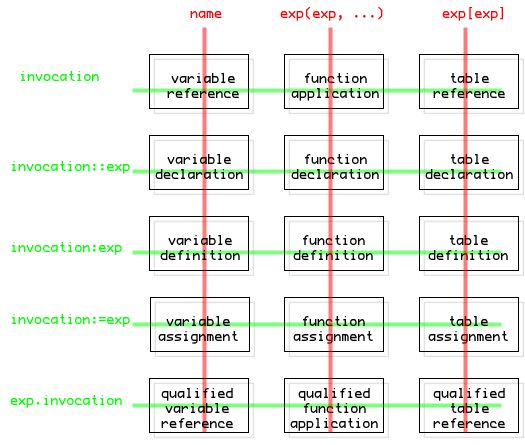
There are five 'operations' or 'language constructions' used to manipulate the "current" dictionary: reference, definition, declaration, assignment and qualification:
The following table summarizes the basic Pico syntax rules. It contrasts the three different invocation kinds with how they can be used to define, assign and refer to values in a Pico program.

There are three footnotes to the table that turn Pico into a powerful programming language: